北京公务员行测-数量关系数学运算
数量运算的题量为15道(北京市),考察主要体现在基础知识的侧重技巧、高频考点必考、扩展考点隔年考察。
数学运算基础必备
算术基础知识
整数的特性
- 质合性
质数:只可以被1和自身整除,不能被其他整数整除。2是唯一的偶质数。
合数:除了1和自身外,还能被其他整数整除。 - 整除的判断
例题:小张的孩子的出生月份乘上29,出生的日期乘上24,所得的两个乘积和为900.问孩子出生在哪一个季度?
解析: 列方程式为29x+24y=900,24、900都可以被12整除,由整除的加减性可知,29x也可以被12整除,那x只能是12,在第四季度。 - 公因数和公倍数
公共的因数、公共的倍数
比例性质
自己分份数后记得不能随便约分。
例题:某公司年终分红,董事会发放奖励,原本打算依据职位高低按甲乙丙比例为3:2:1的方案进行分配,最终决定根据实际贡献按甲乙丙比例为4:3:2分配。最终方案中( )得到的奖金比原有方案有所提升。
解析: 第一次总份数为6,第二次总份数为9,最小公倍数为18。换成9:6:3和8:6:4,所以是丙得到的奖金提高了。
代数工具
不等式
两个正数的算术平均数不小于几何平均数,即(a+b)/2 ≥ √(ab),当且仅当a = b时,等号成立。左边是两个数的算术平均数,右边是几何平均数,这个不等式为均值不等式。
- 两个正数,当他们和为一个确定的数时,他们相等时乘积最大。
- 两个正数,当他们积为一个确定的数时,他们相等时和最小。
例题:用40cmX60cm的砖铺一个房间的地,在不破坏方砖的情况下,正好需要用60块。假设该长方形地面的周长的最小值为X米,那么X的值在以下哪个范围内?
A.X<15 B.15≤X<16
C.16≤X<17 D.X≥17
长方形地面的面积是 60x0.4x0.6=14.4平方米,根据不等式,长宽和最小值为2√14.4,周长最小值为4√14.4,选项为B。
数列
等差数列:如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
an = a1 + (n-1)d
Sn = n*a1+n(n-1)d/2 或 Sn = n(a1+an)/2
等比数列:从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。
an=a₁*qⁿ⁻¹
Sn = a1(1-qⁿ)/(1-q), q≠1
Sn = n*a1, q=1
注:首项! 有时候两者混考,等比数列但是要算加法(e.g.微博关注数)
实战技巧
- 特值法
例题:A、B两个容器装有质量相同的酒精溶液,若从A、B中各取一半的溶液,混合后浓度为45%;若从A取出1/2,B取出1/4溶液,混合后浓度为40%。若从A取出1/5,B取出4/5溶液,混合后浓度为?
解析:设A、B两个容器中的酒精溶液质量都是100,溶液的浓度分别是x、y。则有100x+100y=45%*200, 50x+25y=40%\(50+25),解得x=30%,y=60%。所求为(20*0.3+80*0.6)/100=54% * - 排除法
例题:有A、B两瓶混合液,A中水、油、醋的比例为3:8:5,B中水、油、醋的比例为1:2:3,将A、B两瓶混合液倒在一起后,得到的混合液中水、油、醋的比例可能为()。
A、4:5:2 B、2:3:5
C、3:7:7 D、1:3:3
解析:在A、B中,水的比重都小于醋,混合后也符合,排除A、D;在A、B两瓶混合液中,油的比重分别是1/2,1/3,混合后大于1/3,排除B。
数学运算高频考点
几何问题
平行图行周长和面积
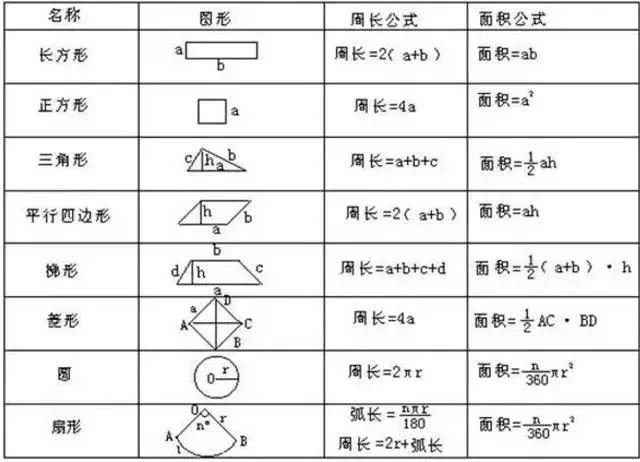
立体图形表面积和体积
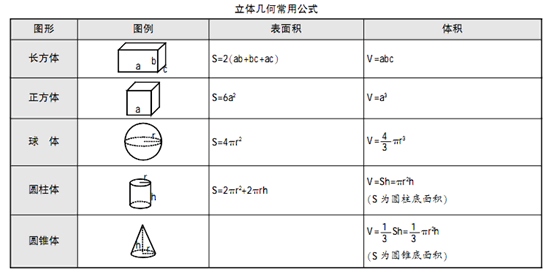
勾股定理
勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。a²+b²=c²
相似三角形
对应边成比例,对应角相等(出现在平行,对顶角图形)
距离最短问题
直线距离最短,立体图形转成平面图画直线。
工程问题
找公倍数>或是工作效率,较为简单。
行程问题
路程 = 速度 * 时间 s = v * t
平均速度 = 总路程 / 总时间
相遇问题
简单相遇问题。 相遇路程 = 速度和 * 相遇时间
例题: A、B从甲地开往乙地,C从乙到甲地,它们同时出发,C与A相遇20分钟后与B相遇。已知A、B、C的速度分别为75千米/小时、60千米/小时、50千米/小时,则甲乙两地的距离是:
解析: 利用甲乙两地的距离列等式,C与A相遇的总路程为甲乙两地的距离,C与B相遇的总路程也是甲乙的距离,(75 + 60)t = (60 + 50)(t + 1/3),t = 22 / 15,再代入,距离为198千米。直线多次相遇。
总路程S = (2n - 1)* s , n表示第n次相遇。